It is important to understand how cryptography can be attacks so that you understand where vulnerabilities might be found and how the incorrect application of cryptography can result in vulnerabilities. We divide these into attack vectors of interest to security architects, and attack vectors of interest to cryptographers. These are different attack vectors.
As a security architect you will need to understand architectural weaknesses that can be exploited by attackers so that you can ensure that your design avoids or mitigates those risks. But as a security architect, you don’t need to worry about subtleties such as related key attacks on symmetric ciphers. This is the concern of cryptographers charged with developing new cryptographic algorithms, or testing existing ciphers. As a security architect your interest is more to follow the news from agencies such as ENISA and NIST who are responsible for making considered recommendations on which algorithms to use (and how), so that should new attack vectors be found by cryptanalysts, you can take their findings into account when you select (or update) the ciphers you are using.
Attack Models
When assessing the strength of a cryptographic system, one starts with the assumption that the attacker knows the algorithm being used. Security by obscurity can provide additional protection (e.g., most military organizations do not willingly disclose their current cryptographic algorithms), but an analysis of a given cryptographic system always starts with the assumption that the algorithm is known.
After that, there are various levels of attack that can be considered, in order of increasing power:
- Ciphertext-only attack: The situation in which the attacker only has access to the encrypted traffic (ciphertext). In many cases, some information about the plaintext can be guessed (such as the language of the message, which can lead to knowledge of the character probability distribution or the format of the message, which can give clues to parts of the plaintext). WEP, the original security algorithm for WiFi, is vulnerable to a number of ciphertext only attacks. By capturing a sufficient number of packets (which typically can be gathered within minutes on a busy network), it is possible to derive the key used in the RC4 stream cipher. It is thought that the 45 million credit cards purloined from the American retail giant T.J. Maxx were obtained by exploiting WEP.
- Known-plaintext attack: The situation when the attacker knows some or all of the plaintext of one or more messages (as well as the ciphertext). This frequently hap- pens when parts of the message tend to be fixed (such as protocol headers or other relatively invariant parts of the messages being communicated). An example of a known-plaintext attack is the famous German Enigma cipher machine, which was cracked in large part by relying upon known plaintexts. Many messages contained the same word in the same place, or contained the same text (e.g. “Nothing to report”), making deciphering the messages possible.
- Chosen-plaintext attack: The situation in which the attacker is able to submit any plaintext the attacker chooses and obtain the corresponding ciphertext. The classic example of a chosen-plaintext attack occurred during WWII when the U.S. intercepted messages indicating the Japanese were planning an attack on a location known as “AF” in code. The U.S. suspected this might be Midway Island, and to confirm their hypothesis they arranged for a plaintext message to be sent from Midway Island indicating that the island’s water purification plant had broken down. When the Japanese intercepted the message and then transmitted a coded message referring to “AF,” the U.S. had the confirmation it needed.
- Chosen-ciphertext attack: When the attacker is able to submit any ciphertext and obtain the corresponding plaintext. An example of this was the attack on SSL 3.0 developed by Bleichenbacher of Bell Labs, which could obtain the RSA private key of a website after trying between 300,000 and 2 million chosen ciphertexts.
There are ciphers that are secure against weaker attacks (e.g. chosen-plaintext) but not against chosen-ciphertext attacks. There are also attacks that are specific to certain types of encryption.
Attacks Primarily of Interest to Cryptographers
The two main mathematical methods of attacking block ciphers are linear cryptanalysis and differential cryptanalysis.
Linear Cryptanalysis
For example, an examination of the cipher might suggest a linear equation that says the second bit of the plaintext, XORed with the fourth and seventh bits of the ciphertext, equals the fifth bit of the key:Linear cryptanalysis was first described by Mitsuru Matsui in 1992. It is a known-plaintext attack that involves a statistical analysis of the operation of the cipher to create linear equations that relate bits in the plaintext, key, and ciphertext.
P2 + C4 + C7 = K5
With a perfect cipher, the above equation would only be true half of the time. If there is a significant bias (i.e. the equation is true significantly more, or significantly less, than half of the time), then this fact can be used to guess, with probability better than 50 percent, the values of some or all of the bits of the key.
By combining a series of such equations it becomes possible to come up with guesses for the key that are far more likely to be correct than simple random guessing, with the result that finding the key is orders of magnitude faster than a simple exhaustive search.
Differential Cryptanalysis
Differential cryptanalysis is a chosen-plaintext attack that was originally developed by Eli Biham and Adi Shamir in the late 1980s and involves comparing the effect of changing bits in the plaintext on the ciphertext output. By submitting carefully chosen pairs of plaintext and comparing the differences between the plaintext pairs with the differences between the resulting ciphertext pairs, one can make probabilistic statements about the bits in the key, leading to a key search space that can be (for a cipher vulnerable to differential analysis) far smaller than an exhaustive search.
Since the development of these two methods, all newly proposed ciphers are tested exhaustively for resistance to these attacks before being approved for use. The AES has been demonstrated to be resistant to such forms of analysis.
Cryptographic Safety Factor
One of the challenges in selecting an appropriate cipher is that there is no way to mathematically measure the security of a cipher in advance of its compromise. In this regard, the estimation of the work factor of a particular algorithm is precisely that—an estimate. In the selection of the algorithm which became the AES, cryptographer Eli Biham introduced the concept of a safety factor. All modern ciphers are built as a series of rounds, each using a subkey derived from the main key.
Cryptographers typically attempt to break ciphers by first attacking a simplified version of the cipher with a reduced number of rounds. For example, early cryptographic attacks on DES (before it fell to simple brute-force) revealed an attack on eight rounds (the full DES has 16 rounds). With AES-256, there is an attack that works on a simplified version of 10 rounds (the full AES has 14 rounds). This was developed after attacks on six-, seven-, and nine-round versions.
The conclusion is that you can expect the attacks to get better over time and that more and more rounds of a cipher will be able to be cracked.
Biham’s safety factor is the ratio of the number of rounds in the cipher, divided by the largest number of rounds that have been successfully attacked so far. While obviously dependent on the level of effort expended by cryptographers trying to undermine a cipher, it is still a useful metric, at least when comparing ciphers that have received sufficient attention from cryptographers.
Using this measure, AES-256 currently has a safety factor of 1.4. Other ciphers, such as Twofish, have greater safety factors, and it was for this reason that the team that developed the Twofish algorithm argued that it ought to have been selected as the AES instead of the algorithm (Rijndael) that was selected.
Attacks of General Interest
In addition to the mathematical analysis of a cipher which aims to detect weaknesses in the algorithm, there are myriad other ways of attacking the use of cryptography which target vulnerabilities in the implementation or use of the cipher. See Figure 3.32.

Brute Force
The simplest attack is to try all possible key values until finding the one that works. In the case of a symmetric cipher, this means a known-plaintext attack in which one tries all possible keys until one has decrypted the ciphertext into something that matches the known plaintext. In many cases, full knowledge of the plaintext is not needed. If one knows the general format of the message, or the language of the message, one can check the output of the decryption against certain heuristics to determine if the output is likely to be the original plaintext (i.e. reading the output to see if it makes sense).
If the encryption algorithm uses 64-bit keys, the attacker starts with 00 00 00 00 00 00 00 0016 and continues until one reaches FF FF FF FF FF FF FF FF16. This can take a while. If your system can decrypt a block of ciphertext and determine if the result is likely to be the desired plaintext in 1 microsecond, going through all possible keys will take roughly 5,800 centuries.
Unfortunately for cryptography, computers get faster every year. In 1998, the Electronic Frontier Foundation (EFF) built a system that could test 90 billion keys per second against the DES cipher, meaning that every possible 56-bit DES key (all 256 or 72,057,594,037,927,936 of them) could be tested in roughly nine days (and, on average, the correct key would be found in half that time).
Obviously, the primary defense against brute-force attacks on symmetric ciphers is key length, which is why the minimum key length for AES is 128 bits. Even if we had a machine a million times faster than the one the EFF built to crack the DES, it would take longer than the universe has been in existence to try every 128-bit key at current processor speeds.
In the case of cryptographically secure hashes (such as are used for securing pass- words), the attack scenario assumes one has a dump of the system’s password file containing all of the passwords encrypted using a secure hash. The attacker then tries to compare the password hashes with guesses to see which passwords can be determined.
The naive approach is to start with “a” and try every combination up to, say, “ZZZZZZZZZZ.” A more sophisticated approach is to have a dictionary of commonly used passwords, typically made up of entries from language dictionaries, combined with combinations of words, letters, and numbers frequently used as passwords (e.g. Password123). After trying all of the entries in a password-cracking word list, the attacker can then start with every possible six-character combination (assuming the system’s minimum password length was six), then every seven-character password, etc., until one runs out of patience (or budget).
This is the method used to analyze the 177 million hashes leaked in the 2016 LinkedIn password breach. Roughly 50 million unique passwords, representing more than 85 percent of the passwords in the file, have been cracked.
There are two defenses against such attacks, neither of which was used by LinkedIn at the time:
- Hashing complexity
- Salting
The LinkedIn password file used SHA1, a fast and efficient hashing algorithm. When it comes to protecting passwords, fast and efficient is exactly what one does NOT want. An eight-GPU password cracking system using 2016 technology can test 69 billion SHA1 hashes per second!
When it comes to password hashing, slower is better, much better. One of the cur- rently recommended algorithms is the Password-Based Key Derivation Function 2 (PBKDF2) — using the same eight-GPU engine, one can only generate 10,000 hashes per second (i.e. roughly 7 million times slower).
The counterattack to slow hashing is a precomputed database of hashes. The attacker takes a dictionary of common passwords (hundreds of millions of passwords from past breaches are freely available online) and every possible password up to, say, eight characters, and runs it through the hashing algorithm in advance. When coming into possession of a breached password file, there is no need to lumber through 10,000 hashes per second; if the password hashes are already known, all that is needed is just to look up each hash.
If the storage space it would take to store these hashes is too large, to compress the hashes at the cost of slightly longer lookup times, the technique called rainbow tables can be used.
The defense against stored dictionary or rainbow table attacks is to combine the pass- word with a unique large random number (called the salt), and then store the combined hash of the password and salt. In this manner, one would have to precompute 2n rainbow tables (if the salt has n bits), so the attack is not feasible.
So the password file contains two fields (in addition to the user’s login name and other metadata):
- The salt
- The output of HASH (salt + password)
To be secure the salt must be:
- Long (at least 16 bytes, and preferably 32 or 64 bytes)
- Random (i.e. the output of a cryptographically secure pseudo-random number generator)
- Unique (calculate a new salt for every user’s password, and a new salt every time the password is changed)
Some go one step further and encrypt the hash using a symmetric cipher, but this is considered to be unnecessary and adds little additional security. In keeping with the nomenclature used in password cryptography, this step is called pepper.
Following the defense-in-depth principle outlined at the beginning of this chapter, one should not rely upon a single security mechanism to provide security. In the world of pass- words, defense in depth typically means multifactor authentication so that a compromise of a password in and of itself does not lead to the compromise of the access management system.
Man-in-the-Middle Attack
An MitM attack requires that the attacker be able to intercept and relay messages between two parties. For example, Mallory wishes to compromise communications between Alice and Bob. Alice wishes to communicate securely with Bob using public key cryptography. Mallory is our attacker. With that in mind, the following takes place (see Figure 3.33):
- Alice sends Bob a message requesting Bob’s public key
- Mallory relays the message to Bob.
- Bob replies with his public key but Mallory intercepts that message and replaces it with Mallory’s public Key.
- Alice, thinking she has Bob’s public key, uses Mallory’s key to encrypt a message (e.g. “Please transfer $10,000 from my account to Acme Company”).
- Mallory intercepts the message, decrypts it (since it was encrypted using her key), tampers with it (e.g. “Please transfer $10,000 from my account to Mallory”), encrypts the tampered message using Bob’s key, and sends the message on to Bob.
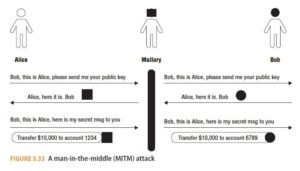
To defend against such attacks, Alice needs to have confidence that the message containing Bob’s key actually originated from Bob (and not the MitM attacker, Mallory). In the case of encrypted HTTPS web traffic, this is done by relying upon public key certificates attested to by a CA (as described earlier in the “Public Key Infrastructure” section). But if the CA is compromised, the attacker can circumvent the identity authentication protections of HTTPS.
In 2011, the compromise of the Dutch CA DigiNotar led to successful MitM attacks against an estimated 300,000 Gmail users.
Side-Channel Attacks
Side-channel attacks involve measuring artifacts of the cryptographic process to deduce information to assist with compromising encrypted information. These artifacts can include:
- Timing
- Cache access
- Power consumption
- Electromagnetic emanations
- Error information
The time taken to encrypt or decrypt a block of data can vary depending on the key or plaintext, and a careful analysis of the time taken to encrypt or decrypt the data can reveal information. The time to perform a cryptographic operation can vary for a number of reasons:
- Conditional branches within the code, which can change the time of execution depending on the branches taken, which in turn depend on the value of the key or plaintext
- CPU instructions that take variable time to complete depending on the operands (e.g. multiplication and division)
- Memory access, which can vary depending on where the data is located (type of memory) or the access history (thus affecting the cache and thus the speed of memory access)
Cache attacks typically involve processes running on different virtual machines on the same physical processor. As the VM performing the encryption is timesliced with the VM running the attacker’s processes, the attacker can probe the processor’s cache to deduce information about the plaintext and the key, and thus compromise the encryption process.
A cache-timing attack was at the heart of the Spectre and Meltdown attacks revealed in 2018 as methods of extracting data from protected regions of a processor’s memory (e.g. keys or plaintext messages).
This type of attack has been most successfully demonstrated against smartcards because of the relative ease with which the device’s power consumption can be monitored, but the attack mechanism has wide applicability.The power consumed by the device performing the cryptographic operation may vary depending on the instructions executed, which in turn depend on the key and data being encrypted. By carefully monitoring the power consumed by the device, it can sometimes be possible to extract information about the key or plaintext.
All electronic systems emit electromagnetic radiation, and it is possible to capture this, sometimes at some distance from the device. These radio signals can sometimes be analyzed to reveal information about the data being processed by the device. Early examples of this type of attack involved analyzing the emanations of cryptographic devices which printed the decrypted message on teletypewriters to determine which characters were being printed.
Countermeasures exist, but in some cases they can be very difficult to implement or can exact a considerable performance penalty. In the case of timing attacks, it is necessary to modify the algorithm so that it is isochronous, which is to say it runs in constant time regardless of the key and data being processed.
The difficulty of implementing a secure algorithm that is secure against side- channel attacks is another reason for the edict discussed earlier: do not write your own cryptographic implementation — use a tested and widely used cryptographic library.
Error information provided (or leaked) by decryption software can provide useful information for attackers. In the Padding Oracle Attack, a system that can be sent any number of test messages, and which generates a distinctive error for encrypted messages that are not properly padded, can be used to decrypt messages without knowing the key. The defense is to report generic errors and not to distinguish between padding errors and other errors.
Birthday Attack
A birthday attack is a method of compromising cryptographic hashes, such as those used for digital signatures. The name is derived from the observation that while the odds that anyone in a group of, say, 23 people has a specific date as their birthday is 23:365 or 6 percent, the odds that there are two people in the group of 23 with the same birthday are 1:1 or 50 percent.
Consider the attacker, Mallory, who wishes to produce a bogus will leaving all of Bob’s worldly goods to Mallory and that appears to have been digitally signed by Bob. Mallory does not know Bob’s secret key so she cannot sign a document. But if she has any signed document from Bob, and can produce a different document which hashes to the same number, she can take the digital signature from the first document, attach it to the second, and it will appear to have been signed by Bob.
But to do this, Mallory would have to generate 2n-1 bogus wills (say, by adding superfluous punctuation, white space, etc.) before she is likely to produce a document that hashes to the same n-bit hash (and can therefore be passed off as having been signed by Bob) – in other words, a hashing collision.
Solving for a hashing collision when one does not care what the hash is, just that one has two different documents with the same hash, is like solving the birthday problem.
Finding two people with the same birthday is a lot easier than finding one person with a specific birthday.
So if Mallory produces both (a) a huge number of wills that express Bob’s real intentions (and which he is willing to sign), and (b) a huge number of wills that express Mallory’s evil intent, she need only produce 2n/2 pairs of wills before she is likely to find a collision. Which is a lot less than 2n-1.
She then gets Bob to digitally sign the real will, and copies the signature to the evil intent version, making it appear to also have been signed by Bob.
Related-Key Attack
A related-key attack is a form of known-ciphertext attack in which the attacker is able to observe the encryption of the same block of data using two keys, neither of which is known to the attacker, but which have a known mathematical relationship.
While it is rare that the attacker can arrange for two mathematically related keys to be used, poor implementations of cryptography can lead to keys being generated that have a known relationship that can be exploited by the attacker. This was the basis for the very successful attack on the WEP security algorithm in the first WiFi standard.
The lessons are twofold: cryptographers need to consider related-key attacks in the design of their ciphers, and security architects need to ensure that the keys they use are well-chosen (by which is meant cryptographically random) and not based on simple mathematical transformations of previously used keys.
Meet-in-the-Middle Attack
A meet-in-the-middle is a known-plaintext attack against block ciphers that perform two or more rounds of encryption. One might think double (or triple) encryption would increase the security in proportion to the combined length of the keys. However, the math behind this doesn’t support the increased complexity.
By creating separate lookup tables that capture the intermediate result (i.e., after each round of encryption) of the possible combinations of both plaintext and ciphertext, it is possible to find matches between values that will limit the possible keys that must be tested in order to find the correct key. This attack, which first came to prominence when it was used to defeat the 2DES algorithm, can be applied to a broad range of ciphers.
Unfortunately, chaining together cryptography algorithms by running them multiple times does not add as much additional security as one might think. With 2DES, the total impact of the second run was to increase complexity from 256 to 257. This has a very small overall impact compared to the work done. The solution to a meet-in-the-middle attack like the one used against 2DES is to do either of the following:
- Add additional rounds of encryption. For example, triple-DES uses three rounds with three different 56-bit keys. While not providing the same security as a 56+56+56 = 168-bit key, it does provide the same as a 112-bit key, which is a lot better than 56 bits.
- Use an algorithm designed to use longer keys. For example, use AES-192 instead of AES-128.
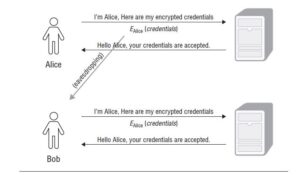
Replay Attack
A replay attack is one in which the attacker does not decrypt the message. Instead, the attacker merely sends the same encrypted message. The attacker hopes that the recipient will assume that the message originated with the authorized party because the information was encrypted.
Alice is trying to log onto a system over an encrypted link. She encrypts her login name and password and then sends the ciphertext to the server. The server decrypts the message, looks up Alice’s password in its authorized user database, verifies the password, and authorizes Alice to access the system.
Mallory is listening on the communications channel and intercepts Alice’s message. Mallory cannot decrypt the message but makes a copy. Later, Mallory sends the saved message to the server, and the server accepts the login, thinking it is talking to Alice.
Note The classic example of a replay attack is breaking into houses by spoofing the garage door opener remote control unit. Early garage door opener remotes worked by sending a secret number to the garage door opener by radio. Thieves could easily tune into the frequency, record the signal, and then replay the same signal at a later time to open the garage door.
Replay attacks can be prevented by ensuring every message can only be accepted by the recipient once. In other words, there must be a method for the recipient to recognize that a message has been replayed. There are many ways to do this, but they all involve including some variable component in the message that can be used to detect a replayed message.
A simple approach is to include a timestamp so that if a message is replayed at a later time, the server can detect that the message is stale. The problems with this approach are (a) it requires Alice and the server to be synchronized, and (b) it still leaves open a short window in which the attacker could replay the message. Consider, the server receives a message at t2 with a timestamp of t1. Even if Alice and the server are perfectly synchronised, t2 will be later than t1 by the latency of the communications channel which typically could have considerable variability. To prevent false negatives (i.e. rejecting valid requests), the server will have to accept messages with timestamps within a certain range (i.e. t2 – t1 < some window of tolerance). If Bob can capture the message and replay it such that it also arrives at the server within the same window, Bob can still succeed.
The approach used to secure automatic garage door openers is for the remote to generate a different code each time the button is pressed. Each opener generates a unique sequence, and the door opener knows the sequence each of the openers authorized to work (“paired”) and keeps track of the last code each remote has used (and therefore the next code that will be accepted). Openers will also “look ahead” in case the remote’s button is pressed when out of range of the garage, resulting in the next code the opener receives not being the next number in sequence.
The problem with this approach is that it depends on the sequence of numbers being unpredictable. If the attacker can eavesdrop on a number of messages, and can reverse-engineer the algorithm that generates the sequence, the remote can be spoofed.
A better approach than timestamps (or random sequences) is for the server to generate a random value and send that to Alice before she sends her login credentials, and for
Alice to incorporate the random value into the encrypted message. For example (and see Figure 3.34):
- Alice asks the server for a login nonce (a number used once, chosen randomly).
- The server generates a cryptographically secure PRNG (see below for the importance of a CSPRNG), encrypts it, and sends it to Alice.
- Alice takes the nonce and packages it with her credentials and sends them back to the server.
- The server decrypts the message and checks that the included nonce matches the one sent to Alice.
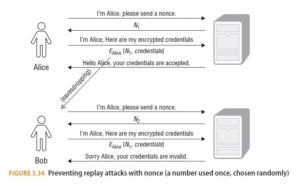
Mallory’s replay attack fails (regardless of how quick she is):
- Mallory asks the server for a login nonce.
- The server generates a nonce that is different from the nonce sent to Alice.
- Mallory doesn’t have Alice’s credentials so cannot use the nonce. Mallory just takes the captured message from Alice and sends it to the server.
- The server decrypts the message and checks that the included nonce matches the one sent to Mallory. It doesn’t and so Mallory’s attempt to login as Alice using a replay attack fails.
The nonce is sometimes called a session ID. It is important that the method used by the server to generate the nonce is unpredictable (which is what is meant by CSPRNG). If Mallory can predict a future nonce, she could intercept a login nonce request from Alice, and send Alice a nonce that she knows the server will generate at some point in the future. Mallory then captures Alice’s credentials (bundled with her nonce). Mallory does not forward the message to the server, the login appears to Alice to time out, and she tries again (at which time Mallory lets the login proceed as normal). Alice chalks it up to a flaky communications channel and thinks nothing more of it. Mallory waits for the time when she has predicted the server would generate the same nonce she sent to Alice, sends a login request to the server, and when the server replies with the nonce Mallory predicted, Mallory just sends the previously captured message from Alice which contains the nonce. And voilà, Mallory logs in as Alice.
Differential Fault Analysis (DFA)
Differential fault analysis (DFA) is a cryptographic attack in which faults are induced in the circuitry performing the cryptographic operation in the expectation that the device can be forced to reveal information on its internal state that can be used to deduce the key.
For example, in 2004 Christophe Giraud published an attack on AES-128 implemented on a smartcard. By using a Xenon strobe, and removing the cover of the smartcard processor, his team was able to induce faults in the execution of the algorithm which enabled them, after multiple induced faults, to derive enough information to determine the full key value.
Quantum Cryptanalysis
Symmetric ciphers are relatively resistant to quantum cryptanalysis, with the best algorithm able to reduce the key search for a 128-bit key from 2128 to 264, and a 256-bit key from 2256 to 2128. While a 264 key search is within the realm of current technology, 2128 is not, and is not likely to be for decades to come, so the solution to defending against quantum cryptography for symmetric ciphers is merely to double the key length.With recent developments in quantum computing, there has been great interest in the ability of quantum computers to break ciphers considered highly resistant to traditional computing methods.
For asymmetric (i.e. public key) ciphers, the problem is much more difficult. Asymmetric ciphers depend on difficult mathematical problems such as factoring very large integers. Unfortunately, these problems are only hard for classical computers. Using quantum computers, integer factorization becomes much easier.
That said, quantum computers have a long way to go before they can compromise currently used public key algorithms. Consider that when this book was written (mid- 2018), the largest integer factored by a quantum computer was 291,311 (e.g. six digits). The integers used in RSA public key systems are recommended to be 2,048 bits in length, or over 600 integer digits.


