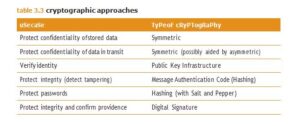
The Cryptographic Methods there are a number of cryptographic tools available to the security architect to protect the confidentiality and integrity of data, the choice of which depends on the threat being defended against, the nature of the communications, and the sensitivity of the information. See Table 3.3 for cryptographic approaches that can be used for different scenarios.
Consider the following different situations:
- Two people (Alice and Bob) wish to communicate confidential information over an insecure channel without unauthorized people being able to eavesdrop on or tamper with the information.
- Alice wishes to send a message to Bob in a manner that Bob has confidence that the message originated with Alice (and not an impostor), and in a manner that Alice cannot later deny having sent the message.
- Bob wishes to store passwords and wants to make sure that the original passwords cannot be obtained even if someone is able to access the file where the passwords are stored, even if the intruder knows the method used to encrypt the password.
The following sections will discuss the various categories of cryptographic algorithms and how they can address the situations described above.
Symmetric Ciphers
Symmetric encryption is the most common approach and the one most people think of when speaking of cryptography. Symmetric encryption takes a message (referred to as the plaintext) and an encryption key and produces output (called the ciphertext) that does not reveal any of the information in the original plaintext. The output can be converted back into the original plaintext if a person has the encryption key that was used to perform the original encryption.
The object is to make it difficult for an eavesdropper who does not know the key to extract any information about the original plaintext from the ciphertext. It is also a necessary property of a secure symmetric cipher that an attacker who comes into possession of examples of plaintext and the related ciphertext cannot deduce the key that was used to encrypt the messages (because if the attacker could do so, all other messages encrypted by that key would then be at risk).
For symmetric encryption to work, both the sender and receiver must share the key. In order for the message to remain confidential, the key must be kept secret. For these reasons, symmetric cryptography is sometimes referred to as secret-key or shared-secret encryption.
The basic types of symmetric cryptography include stream ciphers and block ciphers.
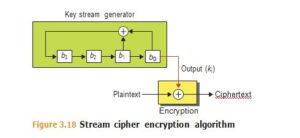
A stream cipher is an encryption algorithm that works one character or bit at a time (instead of a block). They are typically used to encrypt serial communication links and cell-phone traffic, and specifically designed to be computationally very efficient so that they can be employed in devices with limited CPU power, or in dedicated hardware or field programmable gate arrays (FPGAs). See Figure 3.18 where the plaintext flows through the cipher function as a stream, out into ciphertext. At the top of Figure 3.18 is the keystream generator, a constant flow of random bits that are generated one bit at a time. The keystream is a necessity for a stream cipher, relying on these random bits to convert plaintext to ciphertext through an XOR function.
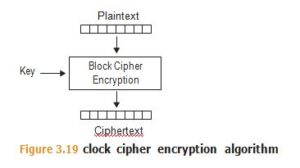
Block ciphers use a deterministic algorithm that takes a fixed-sized block of bits (the plaintext) and a key value, and produces an encrypted block (the ciphertext) of the same size as the plaintext block. Different key values will produce different ciphertexts from the same plaintext. See Figure 3.19.
Although block ciphers are a useful way of dividing ciphers, it is possible to convert nearly all block ciphers into a stream cipher or vice versa.
Stream Ciphers
An example of a simple and provably unbreakable stream cipher is to take a message of length n (the plaintext) and a truly random string of digits of the same length (the key), and combine them as shown in Figure 3.18 to produce the ciphertext.
American cryptographer Claude Shannon proved in 1949 that if the key is truly random, the same length as the plaintext, and only used once then the system is secure and unbreakable (assuming the key remains secret). This type of encryption is called a one- time pad because the key is used for only one round of encrypting and decrypting. The problem with this approach is that the key must be the same length as the message and cannot be reused, making the method completely impractical except for the shortest of messages or for situations (typically government) in which the cost of securely delivering large amounts of key material can be justified. Developments in quantum cryptography (see below), however, will provide methods of securely delivering large amounts of random data that can be used for one-time pad cryptography.
Practical ciphers use a fixed-length key to encrypt many messages of variable length. As we will see in the section on cryptanalysis, some ciphers can be broken if the attacker comes into possession of enough ciphertexts that have been encrypted with the same key. Changing the key periodically so that the amount of ciphertext produced with each unique key is limited can increase the security of the cipher.
Stream ciphers are divided into two types: synchronous and self-synchronizing. Synchronous ciphers require the sender and receiver to remain in perfect synchronization in order to decrypt the stream. Should characters (bits) be added or dropped from the stream, the decryption will fail from that point on. The receiver needs to be able to detect the loss of synchronization and either try various offsets to resynchronize, or wait for a distinctive marker inserted by the sender to enable the receiver to resync.
Self-synchronizing stream ciphers, as the name implies, have the property that after at most N characters (N being a property of the particular self-synchronizing stream cipher), the receiver will automatically recover from dropped or added characters in the cipher- text stream. While they can be an obvious advantage in situations in which data can be dropped or added to the ciphertext stream, self-synchronizing ciphers suffer from the problem that should a character be corrupted, the error will propagate, affecting up to the next N characters. With a synchronous cipher, a single-character error in the ciphertext will only result in a single-character error in the decrypted plaintext.
Block Ciphers
Block ciphers process blocks of n bits at a time, using a key of size k. The output of the processed block then becomes the input for the next iteration of the cipher function. The number of iterations that occur is called the “rounds.” Table 3.4 provides an overview of block ciphers.
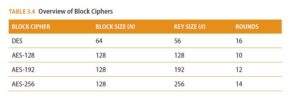
The DES cipher is no longer considered secure because of its short key size, but it introduced the modern age of cryptography and so is historically very important. Because DES was no longer secure, finding its replacement was crucial. Advanced Encryption Standard (AES) was selected after a five-year process to evaluate and select an algorithm from over a dozen candidates.
Most block ciphers, including DES and AES, are built from multiple rounds of mathematical functions, as illustrated in Figure 3.20. While more rounds means greater security, it also slows down the algorithmic process, so the choice is a tradeoff between security and speed.
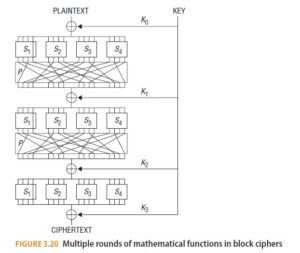
The differences between different block ciphers are in the transformations performed during each round, and the manner in which the encryption key is stretched and then divided to provide a unique key for each round.
There are a couple of standard building blocks used to construct block ciphers, including:
- Substitution or S-boxes (Figure 3.21)
- Permutations or P-boxes (Figure 3.22)
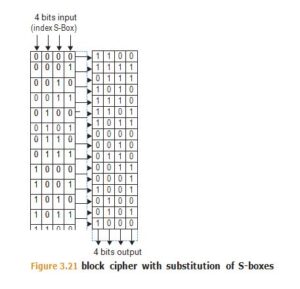
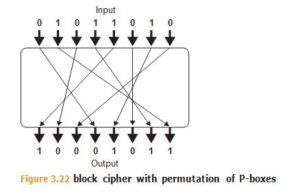
AES uses multiple rounds of substitutions and permutations, while DES uses a 16-round Feistel network.
Block Cipher Modes of Operation
A block cipher such as AES takes eight bytes of plaintext and produces eight bytes of ciphertext. But what if your message is shorter than eight bytes, or longer than eight bytes, or not a multiple of eight bytes?
To handle messages that are not a multiple of the cipher’s block length, one mechanism is to add padding before encryption and remove the padding after encryption. There are many ways to do this, but one approach is to add bytes to the end of the message, each byte containing the count of the number of bytes that have been added (see Figure 3.23). Because the decryption process will examine the last byte of the last block to deter- mine how many padding bytes have been added (and thus need to be removed), if the plaintext is a multiple of the block size, then a final block that just contains padding must be added.
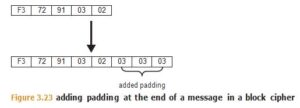
Padding is not without its own risks, such as the Padding Oracle Attack described later in the “Side-Channel Attacks” section.
Once the message has been padded to be an exact multiple of the cipher’s block size, it can be encrypted. The easiest, obvious, and least secure method (for longer messages) is the Electronic Code Book (ECB) mode of operation. In this mode, each block of plaintext is processed independently by the cipher. While this may be adequate for messages that are no greater than the block size, it has serious weaknesses for longer messages, as identical blocks of plaintext will produce identical blocks of ciphertext (Figure 3.24).

The advantage of ECB, apart from its simplicity, is that encryption can be done in parallel (i.e. divided up across multiple processors), and so can decryption. Consequently, an error in one block does not affect subsequent blocks.Even in situations in which the data to be encrypted is the same or smaller than the block size (e.g. a numeric field in a database), use of ECB may be ill-advised if revealing that different rows of the table have the same value might compromise confidentiality. As a trivial example, if one were to use ECB to encrypt the birthdate field, then one could easily determine all the people in the database born on the same day, and if one could determine the birthdate of one of those individuals, you would know the birthdate of all (with the same encrypted birthdate).
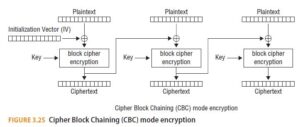
With Cipher Block Chaining (CBC), the first block of data is XORed with a block of random data called the initialization vector (IV). Every subsequent block of plaintext is XORed with the previous block of ciphertext before being encrypted. (See Figure 3.25.)
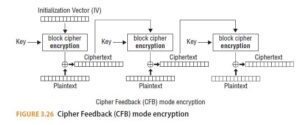
With CFB mode, the IV is encrypted and then XORed with the first block of the plaintext, producing the first block of ciphertext. Then that block of ciphertext is encrypted, and the result is XORed with the next block of plaintext, producing the next block of ciphertext. (See Figure 3.26.)
Because with both CBC and CFB the encryption of block Pn+1 depends on the encryption of block Pn, neither mode is amenable to the parallel encryption of data. Both modes can, however, be decrypted in parallel.
The main differences between CBC and CFB are:
- With CBC, a one-bit change in the IV will result in exactly the same change in the same bit in the first block of decrypted ciphertext. Depending on the application, this could permit an attacker who can tamper with the IV to introduce changes to the first block of the message. This means with CBC it is necessary to ensure the integrity of the IV.
- With CFB, a one-bit change in the IV will result in random errors in the decrypted message, thus this is not a method of effectively tampering with the Message.
- With CBC, the decryption of messages requires the use of the block cipher in decryption mode. With CFB, the block cipher is used in the encryption mode for both encryption and decryption, which can result in a simpler implementation.
The problem with both modes is that encryption cannot be parallelized, and random access is complicated by the need to decrypt block Cn-1 before one can decrypt the desired block Cn.
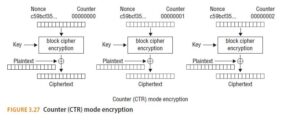
CTR mode addresses this problem by not using previous blocks of the CBC or CFB in producing the ciphertext. (See Figure 3.27.) By using an IV combined with a counter value, one can both parallelize the encryption process and decrypt a single block of the ciphertext. You’ll note that Figure 3.27 includes a nonce value. That unique, randomly generated value is inserted into each block cipher encryption round. Similar to how a random “salt” value is used to ensure different hash values (to prevent comparing to Rain- bow tables), a nonce is unique and is intended to prevent replay attacks.
With all of the modes other than ECB, you need an IV, which either must be communicated to the receiver, or the message must be prefixed by a throw-away block of data (since decryption of a CBC or CFB stream of data without knowing the IV will only cause problems for the first block).
The IV need not be secret (it can be transmitted in plaintext along with the ciphertext) but it must be unpredictable. If an attacker can predict the next IV that will be used, and is able to launch a chosen plaintext attack, then that may enable launching a dictionary attack on the ciphertext.
Coming back to the overarching concept of symmetric encryption, both block and stream ciphers do what most people envision when thinking of cryptography. They turn intelligible text into an unintelligible representation and vice versa. This functions as a closed box without the need for distinguishing between encryption keys and decryption keys, as is the case with asymmetric algorithms.
Hashing
Hashing is the conversion of a block of data into a much smaller value such that the same block of data will convert to the same value. This enables you to verify the integrity of a message you receive by calculating the hash and comparing it against a hash value provided by the sender. Basic hashing is used to accelerate look-up tables and other search functions. Cryptographic hashing is used to protect passwords or to detect tampering of messages. Hash functions perform multiple rounds of mathematical functions to convert data of any size into a mathematical representation of a fixed size (often 160 or 256 bits).
For password protection, the objective is to store a user’s password in a manner that:
- An attacker is unlikely to be able to determine the original password from the hashed value
- An attacker is unlikely to be able to generate a random string of characters that will hash to the same value as the original password (known as a collision)
While necessary conditions for protecting passwords, the above guidelines are not sufficient. Even if the attacker cannot directly deduce the password, just using a cryptographic hash function to convert a password into a shorter fixed-length string leaves the password vulnerable to attack.
Firstly, the attacker can compare the hashed password values to see if the same password has been used by different users (or, if the hash function is widely used, by the same or different users on a different system). This information may be useful in compromising the password.
More seriously, the attacker can construct in advance a table of precomputed hash values from dictionaries and lists of commonly used passwords, and then compare these known hashes with the hash of the unknown password to see if there is a match. This table of precalculated hashes is known as a rainbow table.
To stymie these two attack vectors, you generate a random value for each password to be stored, called the salt, and then add the salt to the password before hashing (by concatenating or other mathematical operation). The salt and the hash are then stored. The salt can be stored in plaintext; it need not be secret, just unpredictable and unique for each password.
When the system authenticates the user, it recomputes the hash from the user’s input and the stored salt, and if the result matches the stored hash, then we know with a high degree of confidence that the user has entered the same password.
By combining a random unique salt with the password, the stored hash will be different from all other hashes using the same password, making precomputed password hash tables useless and obfuscating the reuse of the same password for different accounts or on different systems.
Another attack vector is the brute-force attack. Once the attacker takes the salt and tries different possible passwords in an attempt to obtain a match, it’s more likely the attacker will succeed with matching to hash tables. If the user has chosen a simple or short password, then it matters little which hashing algorithm the security architect has chosen. But if the password is reasonably complex, then the security of the hash will depend on how computationally difficult the hashing algorithm is.
For example, Microsoft used a very simple hashing algorithm in NT LAN Manager (NTLM) and it was possible, using multiple GPU boards, to generate 350 billion pass- word hashes per second, enabling an attacker to try every possible eight-character pass- word in less than seven hours.
LinkedIn used a more secure algorithm, SHA-1, to secure its users’ passwords, but when their password database was breached, high-powered password cracking machines using multiple GPUs were able to break 90 percent of the 6.5 million passwords leaked.
The solution is to select a hashing algorithm that takes so much CPU time that even a multi-GPU password cracking system can only try a limited number of guesses. One such example is the bcrypt, a hashing algorithm based on Blowfish. In 2012, research done by Jeremi Gosney found that the same system that can guess 350,000,000,000 NTLM password hashes per second can only attempt 71,000 bcrypt hashes a second. To put that into perspective, an NTLM password that could be cracked in six hours would take 33 centuries to crack if hashed using bcrypt. With processing power increasing exponentially, and with well-funded attackers able to build far more powerful password-cracking systems, we must assume the above cracking speeds have been vastly increased since Gosney’s work was published.
By selecting an appropriate cryptographic hash function, the security architect can remain confident that even if the password database is compromised, attackers cannot use that to deduce a password (or equivalent string) that can be used to sign on to the system.
The question then becomes: what is an appropriate cryptographic hash function? Appropriate sources of current information on cryptographic algorithms, key and salt lengths, and iteration counts (for password hashing) include the Password Hashing Com- petition (https://password-hashing.net/) and NIST.
Forward Secrecy
An important concept in cryptographic protocol design is that of perfect forward secrecy, also known as forward secrecy. The idea is that the secrecy of past communications will not be compromised, should the long-term keys become known by the attacker. A protocol that has forward secrecy generates unique session keys for every session and then discards them after the session, having generated and shared them in a manner that does not depend upon the long-term keys.
The most well known forward secrecy mechanism is the Diffie-Hellman Key Exchange.
Alice starts by randomly generating two prime numbers, a prime modulus p and a generator g and sends them, in plaintext, to Bob. It does not matter if Mallory is listening.
Alice then generates another random number a which she keeps secret. She then cal- culates: A = ga mod p and sends that number to Bob. Mallory is still listening.
Bob also generates a random number b which he keeps secret. He then calculates B =
gb mod p and sends that to Alice (and perhaps inadvertently to Mallory).
Now comes the magic.
Alice computes the key value K = Ba mod p. Bob computes K = Ab mod p.
The key each has calculated is the same number (see below why) but Mallory, who only knows A, B, g, and p, but not a or b, cannot generate the key.
Alice and Bob then can use any symmetric cipher they choose, with key K, confident that they are the only two who know its value. Furthermore, once they have terminated their communication (session), they discard a, b, A, B, and the key. At that point there is no way for Mallory or anyone else who has recorded the session to decrypt it, even if other keys (private or public) that Alice and Bob may have become known.
Why does the magic work? Due to math.
Alice’s key, Ba mod p is gab mod B (remember how B was calculated) which is the same as gba mod B (it matters not the order of the exponents) which is the same as Ab mod B, which is how Bob calculated the key. Voilà. Alice and Bob have the same (secret) key.
Note that this protocol does nothing to authenticate the identities of Alice or Bob, and therefore is vulnerable to a MitM attack. Imagine Mallory, who can intercept and replace every message between Alice and Bob. In this situation, Mallory can generate one secret key with Alice (who thinks she is talking to Bob), and a second key with Bob(who thinks he is talking to Alice), and then decrypt with one key, and reencrypt with the second key every message between Alice and Bob.
To prevent this, an authentication layer is added using public keys (either shared in advance or via PKI, see below) so that Alice knows it’s Bob and not Mallory she is negotiating a secret key with.
Asymmetric Encryption (Public Key Crytography)
The problem with symmetric encryption is that both parties to the communication (Alice and Bob in our examples) must each know the secret key used to encrypt the data, and if the encrypted data is to remain confidential, no one else must know or be able to guess the secret key. The difficulties of managing and sharing secret keys can make symmetric encryption prohibitively complex as soon as the number of people involved increases beyond a handful.
If there are n people who need to communicate securely using symmetric cryptography, there must be n (n-1) / 2 unique keys, and each person must manage (and arrange to share) n – 1 keys. This is not feasible.
The solution is asymmetric or public key cryptography. The magic of public key cryptography is that instead of having a single secret key that is used to both encrypt and decrypt traffic, you have two keys: a secret private key and a non-secret public key. Data encrypted using a public key cryptography algorithm using one of the keys can only be decrypted using the other key. For example, if Alice encrypts a message to Bob using Bob’s public key, only Bob can decrypt it with his private key. Conversely, if Alice encrypts a message using her secret private key, then anyone can decrypt it since Alice’s public key is, well, public.
Obviously, encrypting a message with a private key alone does nothing to protect the confidentiality of Alice’s message, but it serves a different purpose: it proves that the mes- sage originated from Alice (because who else could have produced it?). This, of course, assumes that Alice’s private key has remained private. But what if it hasn’t? That leads us to the next section on PKI and how public and private keys are managed.
There are a number of public key cryptography algorithms, all based on mathematical functions that are easy to perform in the forward direction but extremely time-consuming to perform in the reverse direction unless a secret is known.
A trapdoor function, as they are called, is one for which computing f(x) is easy, but calculating the inverse function (e.g. determining x if one only knows the value of f(x)) is extremely difficult unless one knows the value of a second variable, y.
The most well-known encryption algorithm based on a trapdoor function is the one first published by Ron Rivest, Adi Shamir, and Leonard Adleman. It is called RSA and is based on the difficulty of factoring large integers.
Choose two large primes p and q and compute:
n = pq
These three numbers are then used to produce the public exponent e and private exponent d. The numbers e and n are made public; e, p, and q are kept secret.
Messages are encrypted with integer modular math on the message using e and n (the public key). Messages are decrypted with similar math but using d (the private key) and n.
The method works because deriving d from n and e is equivalent to finding the two prime factors of n, and if n is a very large semiprime number (i.e. product of two primes of similar size), this is computationally infeasible (at least for non-quantum computers). The largest semiprime factored to date had 232 decimal digits and took 1,500 processor years in 2009. The semiprimes used in RSA have 600 more digits.
Quantum Cryptography
One property of quantum mechanics that lends itself to cryptography is that any attempt to observe or measure a quantum system will disturb it. This provides a basis to transmit a secret encryption key such that if it is intercepted by an eavesdropper, it can be detected. So Alice first sends Bob a secret key using Quantum Key Distribution (QKD) and Bob checks to see if it has been intercepted. If it has, he asks for another key. If it hasn’t, he signals Alice to start sending messages encrypted using a symmetric cipher or a one-time pad and the key, knowing that only Alice and he have access to the key and therefore the communications will remain secret.
As this relies upon a fundamental property of nature, it is immune to advances in computing power or more sophisticated cryptanalytic techniques.
Devices that support QKD are on the market but their high cost and restrictions (such as range) currently limit their adoption. This will change as the technology is improved.


